What runtime does this function have?

void throwHalfOfMyItems(int n) {
    for (int i = 0; i < n; i += 1) {
        if (i % 2 == 0)
            throwItem(n);
    }
}

$ \Theta(n) $

Explanation: The method throwItem() runs n/2 times. Using the simplification rules, we can extract the constant 1/2 to simply get n.

What runtime does this function have?

void lootShulkerBoxes(int n) {
    for (int box = n; box > 0; box -= 1) {
        for (int stack = 0; stack < n; stack += 1) {
            for (int i = 0; i < 64; i += 1) {
                lootItem(i * stack * box);
            }
        }
    }       
}

$ \Theta(n^2) $

Explanation: There are three nested loops in this problem. Whenever there are nested loops whose runtimes are independent of each other, we need to multiply the runtimes in each loop.
So, we get: $\Theta(n * n * 64)$ which simplifies into n^2

I’ve tweaked the previous problem a little 😁 Try to spot the difference and see if it changes the runtime at all!

void lootShulkerBoxes(int n, int stacksToLoot) {
    for (int box = n; box > 0; box -= 1) {
        for (int stack = stacksToLoot; stack > 0; stack -= 1) {
            for (int i = 0; i < 64; i += 1) {
                lootItem(i * stack * box);
            }
        }
    }       
}

$ \Theta(n) $

Explanation: Even though stacksToLoot is a user input, we’re only concerned about finding the runtime for n so stacksToLoot can be treated like a constant! Therefore, we now have $\Theta(n * s* 64)$ where s = stacksToLoot which simplifies into n.

TREEEEEEEEE recursion 🌳🌲🌴

void plantJungleSaplings(int n) {
    if (n > 0) {
        for (int i = 0; i < 4; i += 1) {
            plantJungleSaplings(n - 1);
        }
    }
}

$ \Theta(4^n) $

Explanation: This tree recursion creates a tree with n layers. Each layer you go down, the number of calls multiplies by 4!

This means that the number of calls in total will look like this:

$ \sum_{i=1}^{n}4^i $

And if you remember your power series, you’ll know that this sum is equal to $4^{n+1}-1$ which simplifies into the final answer.

Let’s replace the 4 in the previous problem with n and see what insanity ensues.

void plantCrazySaplings(int n) {
    if (n > 0) {
        for (int i = 0; i < n; i += 1) { // This line changed
            plantCrazySaplings(n - 1);
        }
    }
}

$ \Theta(n!) $

Explanation: This tree recursion creates a tree with n layers. Each layer you go down, the number of calls multiplies by n-1…

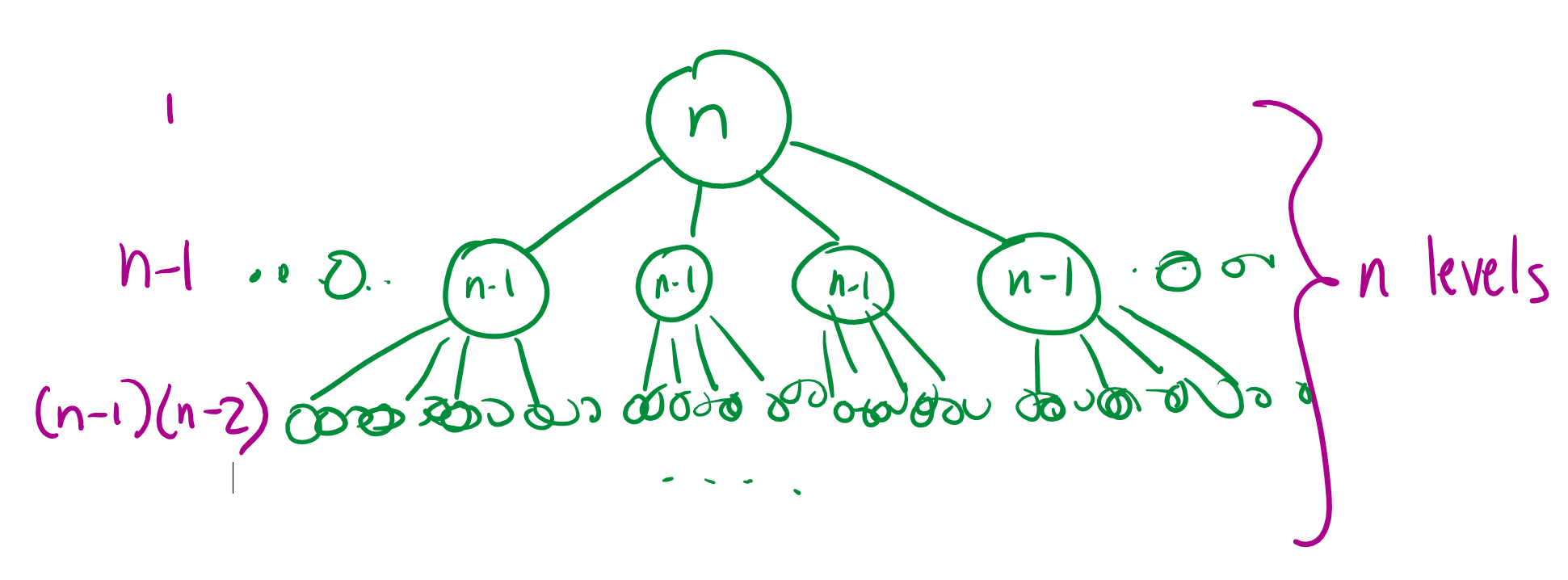
This means that the number of calls in total will look like this:

$ \sum_{i=1}^{n} \frac{n!}{i!} $

Since n! is not dependent on i it can be factored out of the sum to produce this:

$ n!\sum_{i=1}^{n} \frac{1}{i!} $

Hey, that looks a lot like the Taylor series for $e$! Since e is a constant, it simply reduces to n!.

Here’s a case where the best case and worst case runtimes are different. Can you figure out what they are? (Let n = items.length).

Item[] hopperSort(Item[] items) {
    int n = arr.length; 
    for (int i = 1; i < n; ++i) { 
        int key = items[i]; 
        int j = i - 1; 
        while (j >= 0 && items[j].compareTo(key) > 0) { 
            items[j + 1] = items[j]; 
            j = j - 1; 
        } 
        items[j + 1] = key; 
    } 
}

Best Case: $\Theta(n)$ if the array is nearly sorted except for a couple values. In this case, the while loop will only run a small number of times, so the only loop left is the for loop.

Worst Case: $\Theta(n^2)$if the array is totally reversed. This will cause the while loop to run on the order of O(n) times, resulting in a nested loop.

Note: HopperSort is literally just Insertion Sort 😎🤣

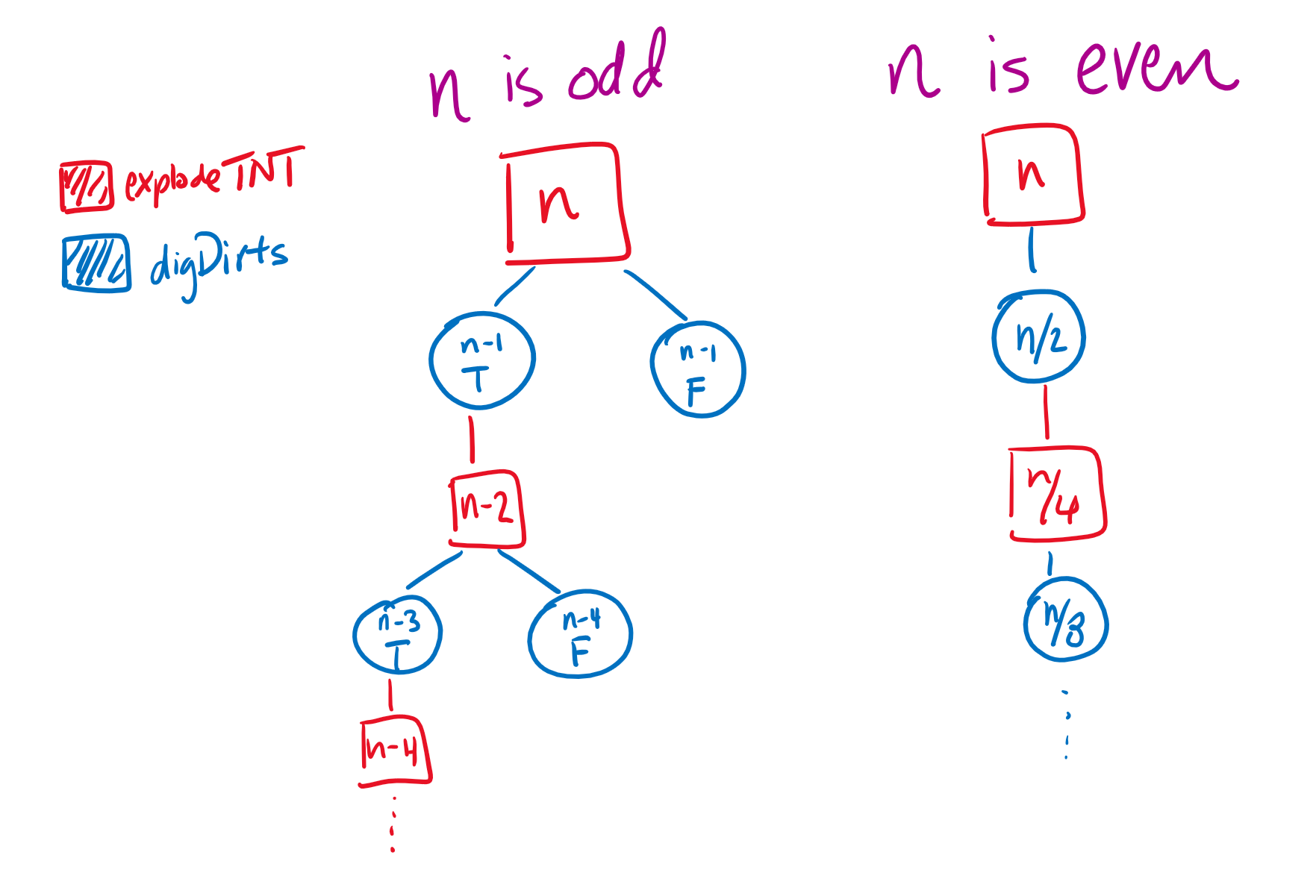
Here’s a mutual recursion problem! What are the best and worst cases for explodeTNT(n)? What are their runtimes?

void explodeTNT(int n) {
    if (n % 2 == 0) {
        digDirts(n - 1, true);
        digDirts(n - 2, false);
    } else {
        digDirts(n / 2, true);
    }
}

void digDirts(int n, boolean isTNT) {
    if (isTNT) {
        explodeTNT(n / 2);
    }
    removeDirt(); // not implemented, assume O(1) runtime
}

Best Case: $\Theta(\log(n))$ if n is even. This will result in n being halved every function call.

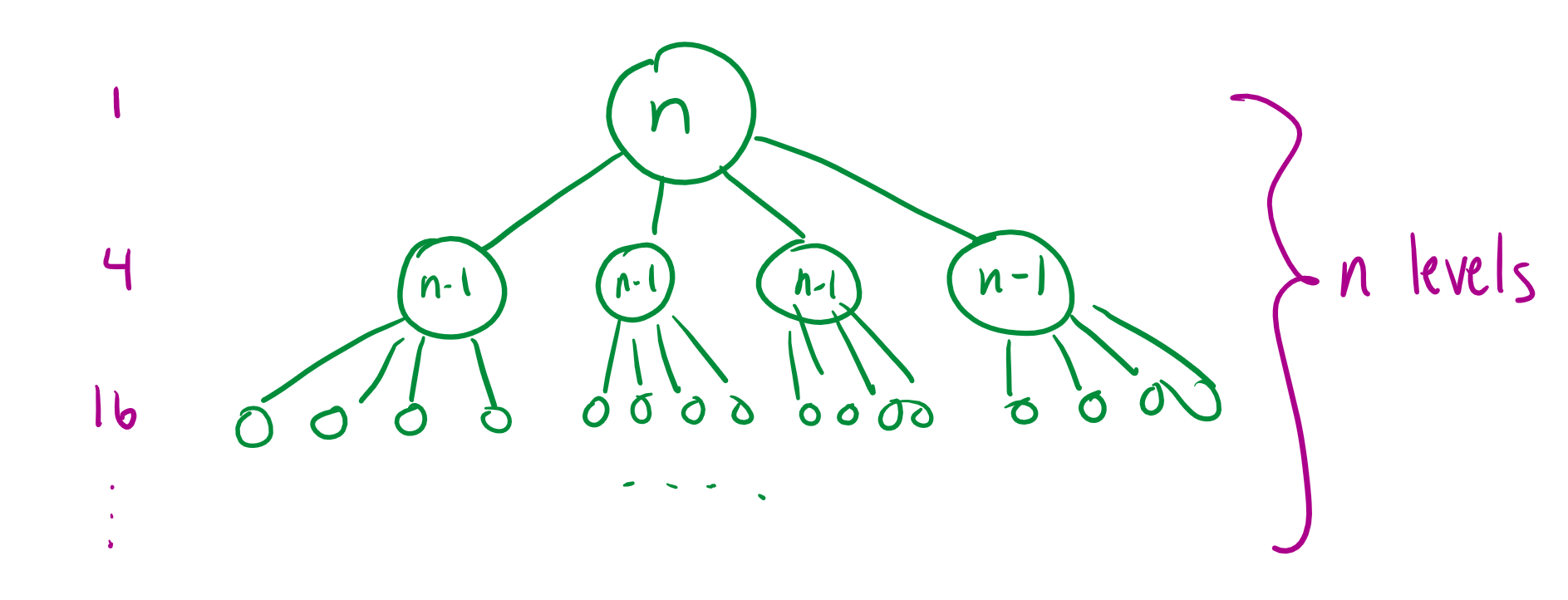
Worst Case: $\Theta(n)$if n is odd. See the tree below for an illustration of what happens in this case- hopefully the diagram will make it clearer as to why it’s O(n).

A huge disaster :ooo

//initially start is 0, end is arr.length.
public int PNH(char[] arr, int start, int end) {
    if (end <= start) {
        return 1;
    }
    int counter = 0; 
    int result = 0;
    for (int i = start; i < end; i += 1) {
        if (arr[i] == 'a') {
            counter += 1;
        }
    }
    for (int i = 0; i < counter; i += 1) {
        result += PNH(arr, start + 1, end);
    }
    int mid = start + (end - start) / 2;
    return PNH(arr, start, mid) + PNH(arr, mid + 1, end);
}

Best Case: $\Theta(n\log(n))$ If none of the characters in char[] is ‘a’, then each call to PNH does $\Theta(n)$ work. Total work per layer is always N, with logN layers total.

Worst Case: $\Theta(n!)$ All of characters in char[] is ‘a’. In this case, the for loop recursive calls will dominate the runtime, because it’ll be the main part of the recursive tree. The interval start to end is decreased by one in the for loop recursive calls, while that interval is halved in the return statement recursive calls. This means the return statement recursive calls will reach the base case in logn levels, while the recursive calls in the for loop will take n levels. Thus, we can proceed with the same analysis as question 4.

Congrats for making it this far! By now you should be an expert in asymptotic analysis :P Here’s one last problem:

//initially start is 0, end is arr.length.
public int lastOne(char[] arr, int start, int end) {
    if (end <= start) {
        return 1;
    }
    else if (arr[start] <= arr[end]) {
        return lastOne(arr, start + 1, end - 1);
    } else {
        int temp = arr[start];
        arr[start] = arr[end];
        arr[end] = temp;

        return lastOne(arr, start + 1, end) 
        + lastOne(arr, start, end - 1) 
        + lastOne(arr, start + 1, end - 1);
    }
}

Best Case: $\Theta(n)$ if the else if case is always true. This will produce a tree with height n/2, where each height does constant work.

Worst Case: $\Theta(3^n)$ if else if case is never true. Sorry no diagram yet :((